Units of Molar Heat Capacity. No Credit Lost. Try Again.

Intensive quantity, estrus capacity per amount of substance

The molar rut capacity of a chemical substance is the amount of energy that must exist added, in the form of rut, to i mole of the substance in order to cause an increase of i unit in its temperature. Alternatively, it is the heat capacity of a sample of the substance divided by the amount of substance of the sample; or also the specific oestrus capacity of the substance times its molar mass. The SI unit of measurement of specific oestrus is joule per kelvin per mole, J⋅Chiliad^−ane⋅mol⁻¹.

Similar the specific oestrus, measured the molar oestrus chapters of a substance, especially a gas, may be significantly higher when the sample is allowed to expand every bit it is heated (at abiding pressure, or isobaric) than when is heated in a closed vessel that prevents expansion (at abiding book, or isochoric). The ratio between the two, however, is the same heat capacity ratio obtained from the respective specific oestrus capacities.

This property is most relevant in chemistry, when amounts of substances are oft specified in moles rather than by mass or volume. The molar estrus capacity by and large increases with the molar mass, often varies with temperature and pressure level, and is different for each state of affair. For example, at atmospheric pressure level, the (isobaric) molar heat capacity of h2o just above the melting point is nearly 76 J⋅K⁻¹⋅mol^−ane, but that of water ice just below that point is near 37.84 J⋅Chiliad^−ane⋅mol⁻¹. While the substance is undergoing a phase transition, such as melting or boiling, its tooth heat capacity is technically space, considering the oestrus goes into changing its state rather than raising its temperature. The concept is non advisable for substances whose precise composition is not known, or whose tooth mass is non well divers, such as polymers and oligomers of indeterminate molecular size.

A closely related property of a substance is the heat capacity per mole of atoms, or atom-molar heat capacity, in which the heat capacity of the sample is divided past the number of moles of atoms instead of moles of molecules. And so, for case, the atom-tooth heat capacity of h2o is 1/3 of its tooth heat capacity, namely 25.three J⋅M^−ane⋅mol^−one.

In informal chemistry contexts, the molar heat capacity may exist chosen but "heat chapters" or "specific heat". Nevertheless, international standards at present recommend that "specific heat capacity" always refer to capacity per unit of measurement of mass, to avoid possible confusion.^[1] Therefore, the discussion "tooth", not "specific", should e'er exist used for this quantity.

Definition [edit]

The molar oestrus capacity of a substance, which may exist denoted by c _m, is the rut capacity C of a sample of the substance, divided by the amount (moles) n of the substance in the sample:

c _grand ${\displaystyle {}\;=\;{\frac {C}{n}}\;=\;{\frac {1}{n}}\lim _{\Delta T\rightarrow 0}{\frac {\Delta Q}{\Delta T}}}$

where ΔQ is the amount of heat needed to raise the temperature of the sample by ΔT. Patently, this parameter cannot be computed when due north is non known or defined.

Like the oestrus capacity of an object, the tooth estrus capacity of a substance may vary, sometimes substantially, depending on the starting temperature T of the sample and the pressure P practical to information technology. Therefore, it should exist considered a part c _{one thousand}(P,T) of those two variables.

These parameters are normally specified when giving the tooth oestrus capacity of a substance. For example, "H_twoO: 75.338 J⋅K^−ane⋅mol⁻¹ (25 °C, 101.325 kPa)" ^[2] When not specified, published values of the molar heat chapters c _k generally are valid for some standard conditions for temperature and pressure.

Nonetheless, the dependency of c _m(P,T) on starting temperature and pressure can often be ignored in practical contexts, eastward.thousand. when working in narrow ranges of those variables. In those contexts one tin can commonly omit the qualifier (P,T), and approximate the molar heat capacity by a abiding c _m suitable for those ranges.

Since the molar heat capacity of a substance is the specific estrus c times the molar mass of the substance K/N its numerical value is generally smaller than that of the specific rut. Alkane wax, for case, has a specific rut of near 2500 J⋅K^−one⋅kg⁻¹ but a molar rut chapters of about 600 J⋅K⁻¹⋅mol⁻ⁱ .

The molar heat capacity is an "intensive" property of a substance, an intrinsic characteristic that does not depend on the size or shape of the amount in consideration. (The qualifier "specific" in front of an extensive holding often indicates an intensive property derived from information technology.^[3])

Variations [edit]

The injection of oestrus free energy into a substance, besides raising its temperature, normally causes an increase in its volume and/or its pressure, depending on how the sample is confined. The choice made most the latter affects the measured tooth rut capacity, even for the same starting pressure P and starting temperature T. Ii particular choices are widely used:

• If the pressure is kept constant (for example, at the ambient atmospheric pressure), and the sample is allowed to expand, the expansion generates work as the force from the pressure displaces the enclosure. That piece of work must come from the heat energy provided. The value thus obtained is said to be the molar heat capacity at constant pressure (or isobaric), and is often denoted c _{P,one thousand}, c _p,m, c _P,thousand, etc.
• On the other hand, if the expansion is prevented — for example past a sufficiently rigid enclosure, or by increasing the external pressure to counteract the internal ane — no work is generated, and the heat energy that would have gone into it must instead contribute to the internal energy of the object, including raising its temperature by an extra amount. The value obtained this style is said to be the molar heat capacity at abiding volume (or isochoric) and denoted c _{V,one thousand}, c _5,1000, c _five,m, etc.

The value of c _Five,m is ever less than the value of c _P,m. This divergence is particularly notable in gases where values under constant pressure are typically xxx% to 66.vii% greater than those at constant book.^[4]

All methods for the measurement of specific heat apply to molar heat chapters as well.

Units [edit]

The SI unit of measurement of molar heat capacity oestrus is joule per kelvin per mole (J/(Thousand⋅mol), J/(Yard mol), J K⁻¹ mol⁻¹, etc.). Since an increment of temperature of one caste Celsius is the same as an increment of one kelvin, that is the same as joule per caste Celsius per mole (J/(°C⋅mol)).

In chemistry, estrus amounts are yet often measured in calories. Confusingly, two units with that name, denoted "cal" or "Cal", have been commonly used to mensurate amounts of heat:

• the "small calorie" (or "gram-calorie", "cal") is 4.184 J, exactly.
• The "grand calorie" (also "kilocalorie", "kilogram-calorie", or "nutrient calorie"; "kcal" or "Cal") is 1000 small calories, that is, 4184 J, exactly.

When heat is measured in these units, the unit of specific oestrus is usually

1 cal/(°C⋅mol) ("small calorie") = iv.184 J⋅1000⁻ⁱ⋅mol^−ane

1 kcal/(°C⋅mol) ("large calorie") = 4184 J⋅Grand⁻¹⋅mol⁻¹.

The molar estrus chapters of a substance has the aforementioned dimension as the heat capacity of an object; namely, L²⋅M⋅T^−two⋅Θ⁻¹, or Thou(50/T)^two/Θ. (Indeed, it is the heat capacity of the object that consists of an Avogadro number of molecules of the substance.) Therefore, the SI unit J⋅K⁻¹⋅mol⁻¹ is equivalent to kilogram metre squared per 2nd squared per kelvin (kg⋅m²⋅Thou⁻¹⋅due south⁻ⁱⁱ).

Physical basis [edit]

Monatomic gases [edit]

The temperature of a sample of a substance reflects the average kinetic energy of its constituent particles (atoms or molecules) relative to its center of mass. Quantum mechanics predicts that, at room temperature and ordinary pressures, an isolated cantlet in a gas cannot shop any pregnant amount of free energy except in the form of kinetic energy. Therefore, when a sure number Northward of atoms of a monatomic gas receives an input ΔQ of rut energy, in a container of fixed volume, the kinetic energy of each atom will increase past ΔQ/North, independently of the atom's mass. This assumption is the foundation of the theory of ideal gases.

In other words, that theory predicts that the tooth estrus chapters at constant book c _{5,one thousand} of all monatomic gases volition be the same; specifically,

c _V,g = iii / two R

where R is the ideal gas constant, virtually 8.31446 J⋅K⁻¹⋅mol⁻¹ (which is the production of Boltzmann's constant k _B and Avogadro'due south number). And, indeed, the experimental values of c _V,m for the noble gases helium, neon, argon, krypton, and xenon (at ane atm and 25 °C) are all 12.5 J⋅K⁻¹⋅mol⁻ⁱ, which is 3 / ii R; even though their diminutive weights range from 4 to 131.

The same theory predicts that the molar heat capacity of a monatomic gas at constant pressure will exist

c _P,m = c _V,thou + R = 5 / 2 R

This prediction matches the experimental values, which, for helium through xenon, are xx.78, 20.79, 20.85, xx.95, and 21.01 J⋅Yard⁻¹⋅mol⁻ⁱ, respectively;^{[5] [half-dozen]} very close to the theoretical 5 / 2 R = 20.78 J⋅Thousand^−ane⋅mol⁻¹.

Therefore, the specific oestrus (per unit of mass, not per mole) of a monatomic gas volition be inversely proportional to its (adimensional) atomic weight A. That is, approximately,

c _Five = (12470 J⋅Thou⁻¹⋅kg⁻ⁱ)/A c _P = (20786 J⋅K⁻¹⋅kg⁻¹)/A

Polyatomic gases [edit]

Vibrations of atoms in a molecule consume some of the heat free energy that otherwise would contribute to the molecule'south kinetic energy.

Degrees of freedom [edit]

A polyatomic molecule (consisting of two or more atoms leap together) can store oestrus free energy in other forms also its kinetic energy. These forms include rotation of the molecule, and vibration of the atoms relative to its center of mass.

These extra degrees of freedom contribute to the molar heat capacity of the substance. Namely, when rut energy is injected into a gas with polyatomic molecules, merely part of it volition go into increasing their kinetic free energy, and hence the temperature; the rest will get to into those other degrees of freedom. Thus, in order to reach the aforementioned increase in temperature, more heat energy will accept to be provided to a mol of that substance than to a mol of a monatomic gas. Substances with loftier atomic count per molecule, like octane, can therefore have a very large heat capacity per mole, and yet a relatively small specific heat (per unit of measurement mass).^{[7] [8] [9]}

If the molecule could be entirely described using classical mechanics, and so the theorem of equipartition of energy could be used to predict that each degree of liberty would have an boilerplate free energy in the corporeality of i / ii kT, where k is Boltzmann'southward constant, and T is the temperature. If the number of degrees of freedom of the molecule is f, and so each molecule would exist property, on average, a total energy equal to 1 / 2 fkT. Then the tooth rut capacity (at constant volume) would be

c _V,grand = 1 / 2 fR

where R is the ideal gas abiding. According to Mayer's relation, the molar heat capacity at constant pressure would be

c _P,chiliad = c _V,m + R = i / 2 fR + R = 1 / 2 (f + two)R

Thus, each boosted degree of freedom will contribute one / two R to the tooth oestrus capacity of the gas (both c _5,thousand and c _P,1000).

In particular, each molecule of a monatomic gas has only f = 3 degrees of freedom, namely the components of its velocity vector; therefore c _5,m = 3 / 2 R and c _P,m = 5 / two R.^[10]

Rotational modes of a diatomic molecule [edit]

For example, the tooth heat capacity of nitrogen North
₂ at constant book is xx.6 J⋅1000⁻¹⋅mol⁻¹ (at 15 °C, ane atm), which is ii.49R.^[xi] From the theoretical equation c _V,m = 1 / 2 fR, one concludes that each molecule has f = 5 degrees of freedom. These turn out to exist three degrees of the molecule'southward velocity vector, plus ii degrees from its rotation about an axis through the center of mass and perpendicular to the line of the two atoms. The degrees of freedom due to translations and rotations are chosen the rigid degrees of freedom, since they do not involve any deformation of the molecule.

Because of those 2 actress degrees of freedom, the tooth heat chapters c _V,yard of N
_two (20.six J⋅K⁻¹⋅mol^−ane) is greater than that of an hypothetical monatomic gas (12.5 J⋅One thousand^−one⋅mol⁻¹) by a gene of 5 / iii .

Frozen and active degrees of freedom [edit]

According to classical mechanics, a diatomic molecule like nitrogen should have more degrees of internal freedom, corresponding to vibration of the ii atoms that stretch and compress the bond between them.

For thermodynamic purposes, each management in which an cantlet can independently vibrate relative to the rest of the molecule introduces two degrees of freedom: one associated with the potential free energy from distorting the bonds, and one for the kinetic free energy of the cantlet'due south motion. In a diatomic molecule like North
_two , there is only one direction for the vibration, and the motions of the 2 atoms must be opposite but equal; then there are only two degrees of vibrational freedom. That would bring f up to 7, and c _V,1000 to iii.5R.

The reason why these vibrations are not absorbing their expected fraction of rut free energy input is provided by quantum mechanics. According to that theory, the energy stored in each degree of freedom must increase or decrease only in certain amounts (quanta). Therefore, if the temperature T of the system is not high enough, the boilerplate energy that would be available for some of the theoretical degrees of freedom (kT/f) may exist less than the corresponding minimum breakthrough. If the temperature is low enough, that may be the case for practically all molecules. 1 then says that those degrees of freedom are "frozen". The tooth heat capacity of the gas volition and then exist determined only by the "agile" degrees of freedom — that, for about molecules, can receive enough energy to overcome that quantum threshold.^[12]

Constant-book specific rut capacity of a diatomic gas (idealised). As temperature increases, heat capacity goes from

3 / two R (translation contribution simply), to

5 / 2 R (translation plus rotation), finally to a maximum of

seven / 2 R (translation + rotation + vibration)

For each degree of freedom, there is an guess critical temperature at which information technology "thaws" ("unfreezes") and becomes active, thus being able to hold oestrus energy. For the three translational degrees of freedom of molecules in a gas, this critical temperature is extremely small, so they can exist assumed to be always active. For the rotational degrees of freedom, the thawing temperature is usually a few tens of kelvins (although with a very calorie-free molecule such every bit hydrogen the rotational energy levels will be spaced so widely that rotational estrus capacity may not completely "unfreeze" until considerably higher temperatures are reached). Vibration modes of diatomic molecules by and large start to actuate only well above room temperature.

In the case of nitrogen, the rotational degrees of freedom are fully active already at −173 °C (100 Thousand, just 23 K to a higher place the boiling signal). On the other hand, the vibration modes only start to become agile around 350 K (77 °C) Accordingly, the tooth heat chapters c _P,chiliad is virtually constant at 29.1 J⋅K^−ane⋅mol⁻¹ from 100 One thousand to about 300 °C. At well-nigh that temperature, it starts to increase rapidly, then it slows down again. It is 35.5 J⋅1000⁻¹⋅mol⁻¹ at 1500 °C, 36.9 at 2500 °C, and 37.5 at 3500 °C.^{[13] [fourteen]} The last value corresponds almost exactly to the predicted value for f = 7.

Constant-book specific rut capacity of diatomic gases (real gases) between about 200 M and 2000 K. This temperature range is not big enough to include both breakthrough transitions in all gases. Instead, at 200 1000, all but hydrogen are fully rotationally excited, so all accept at least

v / 2 R rut capacity. (Hydrogen is already beneath

v / 2 , but it will crave cryogenic conditions for fifty-fifty H_ii to fall to

3 / 2 R). Further, only the heavier gases fully attain

7 / two R at the highest temperature, due to the relatively modest vibrational free energy spacing of these molecules. HCl and H₂ begin to make the transition above 500 Thousand, but have non achieved information technology past 1000 K, since their vibrational free energy level spacing is too wide to fully participate in heat capacity, even at this temperature.

The following is a tabular array of some abiding-pressure molar estrus capacities c _P,grand of various diatomic gases at standard temperature (25 °C = 298 K), at 500 °C, and at 5000 °C, and the credible number of degrees of freedom f ^* estimated by the formula f ^* = 2c _P,yard/R − 2:

	25 °C		500 °C		5000 °C
Gas	c P,m J⋅M−1⋅mol−1	f *	c P,g J⋅K−1⋅mol−one	f *	c P,1000 J⋅Grand−ane⋅mol−1	f *
H2	28.ix	five.0	29.half-dozen	five.1	41.ii	7.9	Non saturated.[15]
CO	29.one	5.0	31.vii	5.6	38.1	7.2	Saturated.[sixteen]
N2	29.1	5.0	31.3	5.5	38.0	seven.1	Saturated.[thirteen]
Cl2	34.0	half dozen.2	37.0	6.nine	39.6	7.five	Max 41.three at ~3700 C.[17]
Br2 (vapour)	(*)36.four	6.8	37.v	7.0	39.2	7.4	Max 41.6 at ~3000 C.[18]

(*) At 59 C (humid point)

The quantum harmonic oscillator approximation implies that the spacing of free energy levels of vibrational modes are inversely proportional to the square root of the reduced mass of the atoms composing the diatomic molecule. This fact explains why the vibrational modes of heavier molecules like Br
_two are active at lower temperatures. The molar rut chapters of Br
₂ at room temperature is consistent with f = 7 degrees of freedom, the maximum for a diatomic molecule. At high enough temperatures, all diatomic gases approach this value.

Rotational modes of single atoms [edit]

Breakthrough mechanics also explains why the specific heat of monatomic gases is well predicted past the ideal gas theory with the assumption that each molecule is a point mass that has simply the f = three translational degrees of liberty.

According to classical mechanics, since atoms have not-zero size, they should also accept iii rotational degrees of liberty, or f = 6 in total. Also, the diatomic nitrogen molecule should have an boosted rotation mode, namely most the line of the two atoms; and thus have f = vi besides. In the classical view, each of these modes should store an equal share of the oestrus free energy.

However, according to breakthrough mechanics, the energy departure between the allowed (quantized) rotation states is inversely proportional to the moment of inertia about the corresponding axis of rotation. Because the moment of inertia of a single atom is exceedingly small, the activation temperature for its rotational modes is extremely loftier. The same applies to the moment of inertia of a diatomic molecule (or a linear polyatomic 1) about the internuclear axis, which is why that mode of rotation is not active in full general.

On the other hand, electrons and nuclei can be in excited states and, in a few exceptional cases, they may be agile even at room temperature, or even at cryogenic temperatures.

Polyatomic gases [edit]

The set of all possible means to infinitesimally readapt the north atoms of a polyatomic gas molecule is a linear infinite of dimension 3n, considering each atom can be independently displaced in each of 3 orthogonal axis directions. However, some three of these dimensions are just translation of the molecule by an infinitesimal displacement vector, and others are just rigid rotations of it past an infinitesimal bending about some axis. Still others may correspond to relative rotation of two parts of the molecule about a unmarried bond that connects them.

The independent deformation modes—linearly independent ways to actually deform the molecule, that strain its bonds—are just the remaining dimensions of this space. Equally in the case diatomic molecules, each of these deformation modes counts every bit 2 vibrational degrees of freedom for energy storage purposes: one for the potential energy stored in the strained bonds, and one for the extra kinetic free energy of the atoms every bit they vibrate nearly the remainder configuration of the molecule.

In detail, if the molecule is linear (with all atoms on a directly line), it has but two not-trivial rotation modes, since rotation about its own axis does not displace any atom. Therefore, it has 3n − five actual deformation modes. The number of energy-storing degrees of freedom is then f = iii + 2 + 2(threen − v) = 6northward − five.

For example, the linear nitrous oxide molecule N≡N=O (with due north = 3) has threen − v = 4 independent infinitesimal deformation modes. Two of them can be described as stretching ane of the bonds while the other retains its normal length. The other two can be identified which the molecule bends at the key atom, in the two directions that are orthogonal to its axis. In each mode, one should presume that the atoms get displaced then that the centre of mass remains stationary and there is no rotation. The molecule then has f = half dozennorthward − 5 = thirteen total free energy-storing degrees of freedom (3 translational, ii rotational, eight vibrational). At high enough temperature, its tooth rut capacity and so should be c _P,grand = 7.five R = 62.63 J⋅Thou⁻ⁱ⋅mol⁻¹. For cyanogen N≡C−C≡N and acetylene H−C≡C−H (due north = iv) the same assay yields f = nineteen and predicts c _P,m = 10.5 R = 87.three J⋅K⁻¹⋅mol⁻ⁱ.

A molecule with north atoms that is rigid and not linear has 3 translation modes and 3 not-niggling rotation modes, hence only 3northward − 6 deformation modes. Information technology therefore has f = 3 + 3 + ii(iiin − 6) = sixn − 6 energy-absorbing degrees of freedom (i less than a linear molecule with the same cantlet count). H2o H_twoO (north = 3) is aptitude in its not-strained land, therefore it is predicted to take f = 12 degrees of freedom.^[19] Methyl hydride CH₄ (north = 5) is tridimensional, and the formula predicts f = 24.

Ethane H₃C−CH₃ (n = eight) has four degrees of rotational freedom: two about axes that are perpendicular to the central bond, and 2 more than because each methyl group can rotate independently about that bond, with negligible resistance. Therefore, the number of independent deformation modes is 3due north − vii, which gives f = 3 + iv + 2(threenorth − 7) = 6n − 7 = 41.

The following table shows the experimental molar oestrus capacities at constant pressure c _P,m of the to a higher place polyatomic gases at standard temperature (25 °C = 298 K), at 500 °C, and at 5000 °C, and the apparent number of degrees of liberty f ^* estimated by the formula f ^* = 2c _P,yard/R − 2:

	25 °C		500 °C		5000 °C
Gas	c P,yard J⋅K−1⋅mol−1	f *	c P,k J⋅Thou−1⋅mol−one	f *	c P,m J⋅Thou−1⋅mol−1	f *	f	Notes
N≡N=O	38.vi	7.3	51.8	10.5	62.0	12.9	13	[20]
Northward≡C–C≡Due north	56.7	11.six	72.iii	15.4	86.7	18.ix	19	[21]
H–C≡C–Northward	44.0	8.vi	63.2	13.2	92.9	20.three	xix	[22]
HtwoO	—	—	38.iv	seven.2	59.7	12.4	12	[23]
CH4	35.vii	6.6	61.6	12.viii	105.7	23.iv	24	[24]
HthreeC–CH3	52.5	10.six	105.6	23.iv	168.7	(*)38.6	41	[25]

(*) At 3000C

Specific estrus of solids [edit]

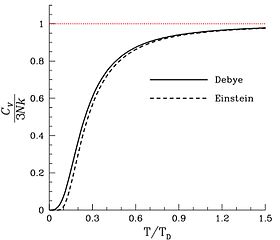
The dimensionless oestrus capacity divided by 3, as a part of temperature as predicted past the Debye model and by Einstein'due south before model. The horizontal axis is the temperature divided by the Debye temperature. Notation that, as expected, the dimensionless heat capacity is nil at accented zero, and rises to a value of three every bit the temperature becomes much larger than the Debye temperature. The red line corresponds to the classical limit of the Dulong–Petit law

In nearly solids (but not all), the molecules have a stock-still mean position and orientation, and therefore the only degrees of freedom available are the vibrations of the atoms.^[26] Thus the specific rut is proportional to the number of atoms (not molecules) per unit of mass, which is the Dulong–Petit law. Other contributions may come from magnetic degrees of freedom in solids, just these rarely make substantial contributions.^[27] and electronic^[28] Since each atom of the solid contributes one independent vibration mode, the number of degrees of freedom in n atoms is half dozenn. Therefore, the rut chapters of a sample of a solid substance is expected to be iiiRN _a, or (24.94 J/K)North _a, where N _a is the number of moles of atoms in the sample, not molecules. Said another way, the atom-molar heat capacity of a solid substance is expected to be threeR = 24.94 J⋅One thousand⁻¹⋅mol⁻¹, where "amol" denotes an amount of the solid that contains the Avogadro number of atoms.^[29]

It follows that, in molecular solids, the heat capacity per mole of molecules will unremarkably be close to 3nR, where due north is the number of atoms per molecule.

Thus due north atoms of a solid should in principle store twice as much energy as northward atoms of a monatomic gas. 1 way to wait at this result is to detect that the monatomic gas tin can only shop energy every bit kinetic energy of the atoms, whereas the solid can store it also every bit potential energy of the bonds strained by the vibrations. The atom-molar heat capacity of a polyatomic gas approaches that of a solid every bit the number due north of atoms per molecule increases.

Equally in the example f gases, some of the vibration modes volition be "frozen out" at depression temperatures, specially in solids with calorie-free and tightly bound atoms, causing the cantlet-molar heat capacity to be less than this theoretical limit. Indeed, the cantlet-molar (or specific) heat chapters of a solid substance tends toward zero, as the temperature approaches absolute zero.

Dulong–Petit law [edit]

Every bit predicted by the to a higher place analysis, the estrus capacity per mole of atoms, rather than per mole of molecules, is found to be remarkably constant for all solid substances at high temperatures. This relationship was noticed empirically in 1819, and is called the Dulong–Petit constabulary, after its two discoverers.^{[30] [31]} This discovery was an important argument in back up of the atomic theory of matter.

Indeed, for solid metallic chemic elements at room temperature, atom-tooth oestrus capacities range from about 2.8 R to three.4 R. Large exceptions at the lower end involve solids equanimous of relatively low-mass, tightly bonded atoms, such equally beryllium (two.0 R, but of 66% of the theoretical value), and diamond (0.735 R, only 24%). Those conditions imply larger breakthrough vibrational free energy spacing, thus many vibrational modes are "frozen out" at room temperature. H2o ice close to the melting indicate, too, has an anomalously low heat capacity per cantlet (1.5 R, just 50% of the theoretical value).

At the higher end of possible heat capacities, estrus capacity may exceed R past small-scale amounts, due to contributions from anharmonic vibrations in solids, and sometimes a pocket-size contribution from conduction electrons in metals. These are not degrees of freedom treated in the Einstein or Debye theories.

Specific heat of solid elements [edit]

Sincethe bulk density of a solid chemical chemical element is strongly related to its molar mass, in that location exists a noticeable inverse correlation between a solid's density and its specific heat capacity on a per-mass basis. This is due to a very gauge tendency of atoms of most elements to be about the same size, despite much wider variations in density and diminutive weight. These 2 factors (constancy of atomic volume and continuance of mole-specific heat capacity) result in a good correlation betwixt the volume of whatever given solid chemical chemical element and its total heat capacity.

Some other manner of stating this, is that the volume-specific rut chapters (volumetric heat capacity) of solid elements is roughly a abiding. The molar volume of solid elements is very roughly constant, and (even more reliably) then also is the molar rut capacity for nigh solid substances. These 2 factors determine the volumetric heat capacity, which as a bulk property may be hit in consistency. For example, the element uranium is a metal that has a density almost 36 times that of the metal lithium, but uranium's specific oestrus capacity on a volumetric ground (i.due east. per given volume of metallic) is only 18% larger than lithium's.

Nonetheless, the boilerplate atomic volume in solid elements is not quite constant, so there are deviations from this principle. For example, arsenic, which is but 14.5% less dumbo than antimony, has nigh 59% more specific heat capacity on a mass footing. In other words; fifty-fifty though an ingot of arsenic is only near 17% larger than an antimony i of the aforementioned mass, it absorbs about 59% more heat for a given temperature rise. The heat capacity ratios of the two substances closely follows the ratios of their molar volumes (the ratios of numbers of atoms in the same volume of each substance); the difference from the correlation to uncomplicated volumes, in this example, is due to lighter arsenic atoms being significantly more closely packed than antimony atoms, instead of like size. In other words, like-sized atoms would cause a mole of arsenic to be 63% larger than a mole of antimony, with a correspondingly lower density, allowing its volume to more closely mirror its heat capacity behavior.

Effect of impurities [edit]

Sometimes small impurity concentrations tin can greatly affect the specific heat, for instance in semiconducting ferromagnetic alloys.^[32]

Specific rut of liquids [edit]

A full general theory of the rut capacity of liquids has not withal been achieved, and is notwithstanding an agile expanse of research. Information technology was long thought that phonon theory is not able to explain the rut chapters of liquids, since liquids only sustain longitudinal, merely non transverse phonons, which in solids are responsible for two/3 of the heat chapters. However, Brillouin handful experiments with neutrons and with X-rays, confirming an intuition of Yakov Frenkel,^[33] have shown that transverse phonons do be in liquids, albeit restricted to frequencies above a threshold called the Frenkel frequency. Since most energy is contained in these high-frequency modes, a uncomplicated modification of the Debye model is sufficient to yield a good approximation to experimental oestrus capacities of elementary liquids.^[34]

Because of high crystal binding energies, the effects of vibrational manner freezing are observed in solids more often than liquids: for instance the heat capacity of liquid h2o is twice that of ice at near the same temperature, and is again close to the iiiR per mole of atoms of the Dulong–Petit theoretical maximum.

Amorphous materials tin exist considered a type of liquid at temperatures higher up the glass transition temperature. Below the glass transition temperature amorphous materials are in the solid (glassy) state form. The specific heat has characteristic discontinuities at the glass transition temperature which are acquired by the absence in the glassy land of percolating clusters made of broken bonds (configurons) that are present only in the liquid phase.^[35] Above the glass transition temperature percolating clusters formed by broken bonds enable a more than floppy construction and hence a larger caste of freedom for atomic motion which results in a higher heat capacity of liquids. Below the glass transition temperature there are no extended clusters of cleaved bonds and the heat capacity is smaller because the solid-state (glassy) structure of amorphous material is more rigid. The discontinuities in the heat capacity are typically used to detect the glass transition temperature where a supercooled liquid transforms to a glass.

Effect of hydrogen bonds [edit]

Hydrogen-containing polar molecules like ethanol, ammonia, and h2o have powerful, intermolecular hydrogen bonds when in their liquid phase. These bonds provide another place where oestrus may be stored as potential energy of vibration, fifty-fifty at comparatively low temperatures. Hydrogen bonds account for the fact that liquid water stores nigh the theoretical limit of 3R per mole of atoms, even at relatively low temperatures (i.eastward. nearly the freezing point of water).

Run into besides [edit]

• Breakthrough statistical mechanics
• Heat capacity ratio
• Statistical mechanics
• Thermodynamic equations
• Thermodynamic databases for pure substances
• Heat equation
• Heat transfer coefficient
• Heat of mixing
• Latent heat
• Material properties (thermodynamics)
• Joback method (Estimation of heat capacities)
• Specific oestrus of melting (Enthalpy of fusion)
• Specific estrus of vaporization (Enthalpy of vaporization)
• Volumetric rut chapters
• Thermal mass
• R-value (insulation)
• Storage heater
• Frenkel line

References [edit]

1. ^ International Bureau of Weights and Measures (2006), The International Organization of Units (SI) (PDF) (8th ed.), ISBN92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-xvi
2. ^ W. Wagner, J. R. Cooper, A. Dittmann, J. Kijima, H.-J. Kretzschmar, A. Kruse, R. Mare, M. Oguchi, H. Sato, I. Stöcker, O. Šifner, Y. Takaishi, I. Tanishita, J. Trübenbach and Thursday. Willkommen (2000): "The IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam", ASME J. Eng. Gas Turbines and Power, volume 122, pages 150–182
3. ^ International Spousal relationship of Pure and Applied Chemistry, Physical Chemistry Partition. "Quantities, Units and Symbols in Physical Chemical science" (PDF). Blackwell Sciences. p. seven. The adjective specific before the name of an extensive quantity is often used to mean divided by mass.
4. ^ Lange's Handbook of Chemistry, 10th ed. p. 1524
5. ^ Shuen-Chen Hwang, Robert D. Lein, Daniel A. Morgan (2005). "Noble Gases". Kirk Othmer Encyclopedia of Chemical Technology. Wiley. pp. 343–383. |doi=10.1002/0471238961.0701190508230114.a01.pub2
6. ^ Hwang, Shuen-Cheng; Weltmer, William R. (2000). "Helium Group Gases". Kirk-Othmer Encyclopedia of Chemical Technology. Wiley. pp. 343–383. doi:10.1002/0471238961.0701190508230114.a01. ISBN0-471-23896-ane.
7. ^ Feynman, R., Lectures in Physics, vol. I, chapter forty, pp. seven–8
8. ^ Reif, F. (1965). Fundamentals of statistical and thermal physics . McGraw-Hill. pp. 253–254. ISBN9780070518001.
9. ^ Charles Kittel; Herbert Kroemer (2000). Thermal physics. Freeman. p. 78. ISBN978-0-7167-1088-2.
10. ^ Textbook: Young and Geller College Physics, 8e, Pearson Education, 2008
11. ^ Steven T. Thornton and Andrew King (1993): Modern Physics for Scientists and Engineers, Saunders College Publishing, 1993
12. ^ Breakthrough Physics and the Physics of large systems, Part 1A Physics, University of Cambridge, C.G. Smith, 2008.
13. ^ ^{a b} "Nitrogen" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-xviii.
14. ^ M.Due west. Chase Jr. (1998) NIST-JANAF Themochemical Tables, Fourth Edition, In Periodical of Concrete and Chemic Reference Data, Monograph 9, pages 1–1951.
15. ^ "Hydrogen" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
16. ^ "Carbon monoxide" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
17. ^ "Chlorine"" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-eighteen.
18. ^ "Bromine" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
19. ^ Smith, C. G. (2008). Breakthrough Physics and the Physics of large systems, Office 1A Physics. University of Cambridge.
20. ^ "Nitrous oxide" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
21. ^ "Cyanogen" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-eighteen.
22. ^ "Acetylene" NIST Chemical science WebBook, SRD 69, online. Accessed on 2019-05-18.
23. ^ "Water" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
24. ^ "Methane" NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
25. ^ "Ethane" NIST Chemistry WebBook, SRD 69
26. ^ Kittel, Charles (2005). Introduction to Solid State Physics (eighth ed.). Hoboken, New Bailiwick of jersey, United states of america: John Wiley & Sons. p. 141. ISBN978-0-471-41526-viii.
27. ^ Blundell, Stephen (2001). Magnetism in Condensed Thing . Oxford Primary Series in Condensed Matter Physics (1st ed.). Hoboken, New Jersey, United states: Oxford University Press. p. 27. ISBN978-0-19-850591-four.
28. ^ Kittel, Charles (2005). Introduction to Solid Land Physics (eighth ed.). Hoboken, New Jersey, The states: John Wiley & Sons. p. 141. ISBN978-0-471-41526-8.
29. ^ "The Rut Capacity of a Solid" (PDF). Archived from the original (PDF) on 2014-02-11.
30. ^ Petit A.-T., Dulong P.-L. (1819). "Recherches sur quelques points importants de la Théorie de la Chaleur". Annales de Chimie et de Physique. 10: 395–413.
31. ^ Petit A.-T., Dulong P.-50.: Recherches sur quelques points importants de la Théorie de la Chaleur. In: Annales de Chimie et de Physique 10, 395–413 (1819) (Translation)
32. ^ Hogan, C. (1969). "Density of States of an Insulating Ferromagnetic Alloy". Physical Review. 188 (two): 870. Bibcode:1969PhRv..188..870H. doi:10.1103/PhysRev.188.870.
33. ^ In his textbook Kinetic Theory of Liquids (engl. 1947)
34. ^ Bolmatov, D.; Brazhkin, V. V.; Trachenko, K. (2012). "The phonon theory of liquid thermodynamics". Scientific Reports. 2: 421. arXiv:1202.0459. Bibcode:2012NatSR...2E.421B. doi:10.1038/srep00421. PMC3359528. PMID 22639729.
    • Hamish Johnston (13 June 2012). "Phonon theory sheds light on liquid thermodynamics". Physics World.
35. ^ Ojovan, Michael I.; Lee, William E. (2006). "Topologically disordered systems at the glass transition" (PDF). Journal of Physics: Condensed Matter. 18 (l): 11507–11520. Bibcode:2006JPCM...1811507O. doi:10.1088/0953-8984/18/50/007.

padillafroasur.blogspot.com

Source: https://en.wikipedia.org/wiki/Molar_heat_capacity

Share this post